- Internal energy is the sum of the randomly distributed kinetic and potential energies of the particles in a body
- Kinetic energy depends on temperature
- Potential energy depends on intermolecular forces
- Ideal gases have no intermolecular forces so internal energy is only dependant on kinetic energy
- Particles move in random directions with a range of kinetic energies
U = Σ(kinetic energies) + Σ(potential energies)
First law of thermodynamics
The internal energy of a system is increased when energy is transferred to it by heating or when work is done on it (and vice versa).
ΔU = ΔQ – ΔW
Increases in internal energy = thermal energy added to system – work done by system
Changes of state and temperature
Q = mcΔθ
Q = thermal energy (J)
m = mass (kg)
c = specific heat capacity (Jkg⁻¹K⁻¹)
Δθ = temperature change (K)
Specific heat capacity is the thermal energy required to increase the temperature of 1kg of a material by 1K.
The change in Kelvin is the same as the change in Celsius as they increase/decrease at the same rate.
Specific latent heat is the amount of thermal energy required to change the state of 1kg of a material, without a change in temperature (usually at a pressure of 1 atm).
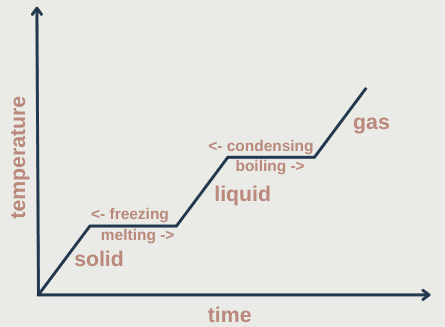
As temperature increases, the mean kinetic energy of particles increases so the total kinetic energy increases. Similarly, the mean potential energy increases as on average atoms move further apart. Some of the intermolecular forces are weakened causing a change of state – the temperature remains constant as the energy is going into loosening the intermolecular forces.
Q = ml
Q = Thermal energy required to change the state of a substance without a change in temperature (J)
m = mass (kg)
l = specific latent heat (Jkg⁻¹)
Specific latent heat of vaporisation involves the change in state from liquid to gas and vice versa.
Specific latent heat of fusion deals with the change is state from solid to liquid and liquid to solid.
Use the following values for the question below:
Specific heat capacity of ice = 2.10 kJkg⁻¹K⁻¹
Latent heat of fusion of water = 334 kJkg⁻¹
Specific heat capacity of water = 4.20 kJkg⁻¹K⁻¹
Latent heat of vaporisation of water = 2260 kJkg⁻¹
How much energy is needed to convert 5kg of ice at -20°C to water vapour at 100°C?
First we need to calculate the energy required to heat the ice to its melting point (0°C):
Q = mcΔθ
Q = 5 x 2.10 x (20)
Q = 210 kJ
Now we need to calculate the thermal energy required to melt the ice:
Q = ml
Q = 5 x 334
Q = 1670 kJ
Next, we need to heat the water to 100°C:
Q = 5 x 4.20 x 100
Q = 2100 kJ
Finally, we are calculating the thermal energy required to vaporise the water:
Q = ml
Q = 5 x 2260
Q = 11300 kJ
The total energy required is the sum of all of these values:
210 + 1670 + 2100 + 11300 = 15280 kJ
If the heater used is a 12kW heater, how long does it take to convert the ice to water vapour?
12kW = 12000 W
P = E/t
t = E/P
t = (15280 x 1000)/12000 = 1273 seconds = 21 minutes
Continuous flow
A continuous flow method can be used to calculate the specific heat capacity of a fluid (liquid or gas). A fluid with mass m₁ moves over an electric heater at a constant rate and the initial and final temperatures are recorded. The flow rate is then altered to give a different mass (m₂) and the experiment is repeated. Specific heat capacity can be calculated by assuming the thermal energy lost to the surroundings is constant for both flow rates.
The electrical energy supplied to the fluid in time t₁ is equal to the thermal energy plus the thermal energy lost to the surroundings:
I₁V₁t₁ = m₁cΔθ + E (lost)
as P = IV and E = Pt,
E = IVt
The equation for the second flow rate is the same:
I₂V₂t₂ = m₂cΔθ + E (lost)
The thermal energy lost, E (lost), is assumed to be the same in both experiments so they can be subtracted from each other to give:
I₁V₁t₁ – I₂V₂t₂ = m₁cΔθ – m₂cΔθ
I₁V₁t₁ – I₂V₂t₂ = cΔθ(m₁ – m₂)
If the time is the same for both experiments:
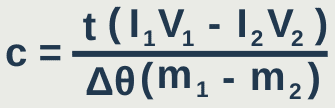
Ideal gases
Assumptions:
- An ideal gas consists of a large number of identical, small, spherical molecules
- Volume of molecules is a lot smaller than volume of container
- Distance between molecules is a lot larger than the size of the molecules
- All collisions are elastic (kinetic energy is conserved) and frictionless
- Movements of molecules obey Newton’s laws of motion
- Molecules are constantly moving in random directions
- No intermolecular forces
- Time spent between collisions is much larger than time spent colliding
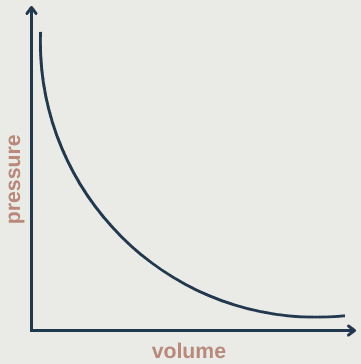
Boyle's law
- Describes relationship between pressure and volume of a fixed mass of gas at a constant temperature
- The pressure is caused by gas molecules bumping into the walls of the container
- Pressure is inversely proportional to volume (at constant temperature): p ∝ 1/V
pV = constant
p₁V₁ = p₂V₂
Graph is asymptopic:
Charles' law
- At a fixed pressure, the volume of a gas is proportional to the temperature of the gas
- When the gas is heated the particles move faster and further apart from each other, to equalise the pressure, the volume of the gas increases
V ∝ T at a fixed pressure and mass
V/T = constant
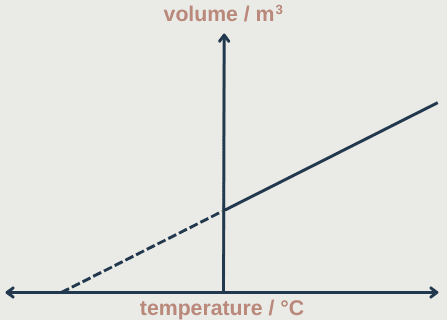
The volume of a gas can be measured at different temperatures (constant pressure and mass) and plotted on a graph. The line can then be extrapolated backwards to estimate the value of absolute zero.
Absolute zero is the temperature at which pressure and volume fall to zero and particles stop moving. It is equal to 0K = -273°C
