- Electric field strength is the force per unit charge
- Units NC⁻¹ or Vm⁻¹
- It is a vector quantity
- The direction of the field is the direction a positive charge would move in
- Density of field lines indicates field strength (closer together = stronger field)
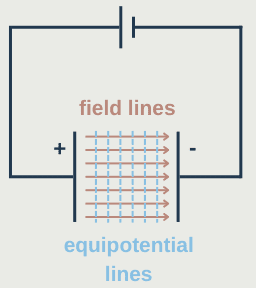
The diagram above shows a uniform electric field between two parallel plates. The straight field lines are equal distances apart. Equipotential lines are also equally spaced and perpendicular to the field lines.
Potential difference is the energy transferred per unit charge so, a volt is a joule per coulomb (JC⁻¹).
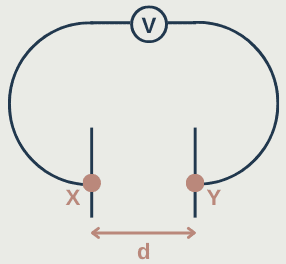
To move a charge q from X to Y, the force on the charge due to the electric field F = E x Q (where E is the electric field strength) must be equal in magnitude to the work done in moving the charge.
Work done = F x d.
Work done = EQ x d
The work done is also equal to the energy gained by the charge moving through a potential difference, work done = QV.
EQd = QV
Ed = V
E = V / d
This shows that electric field strength can also be measured in Vm ⁻¹.
Applications of Uniform Electric Fields
The diagram below shows a charged particle (e.g an electron) suspended in a vertical electric field. The charged plates have a distance d between them and a potential difference of V. Here, the gravitational field strength would be equal in magnitude but opposite in direction to the force on the charge due to the electric field.
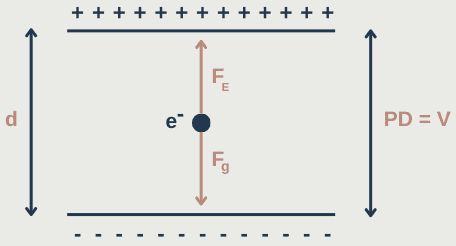
FE = Fg
Ee = me/g (F = EQ, in this case Q = charge on electron = e)
g/E = e/me (e/me is the specific charge of the electron)
By substituting in E = V/d, we get e/me = gd/V
Here we have an electron being accelerated in a uniform electric field. The electron has an initial velocity u and mass me. The force on the electron can be found using F = EQ and E = V/d. It will travel in a straight line as the as the acceleration due to the electric field is constant.
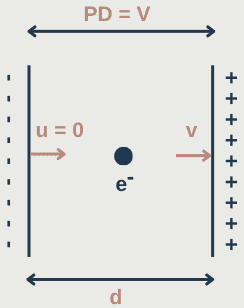
Find an equation for the final velocity v:
As the work done on the electron by the electric field is equal to the change in kinetic energy of the electron, we can set them equal to each other.
Work done on electron = Fd = QV
1/2 mv² = eV/d
Rearrange to find v:
v = √(2eV/mₑd)
As E = V/d
v = √(2Ee/mₑ)
A charged sphere is suspended in a uniform electric field:
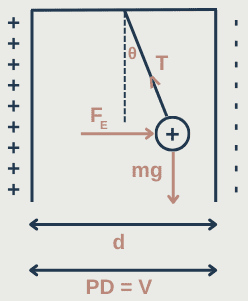
FE = force due to the electric field
For a charged sphere, charge may be considered to be at the centre.
We can resolve vertically and horizontally to form an equation:
R(H): Tsinθ = FE = qV/d
R(V): Tcosθ = Fg = mg
Tsinθ/Tcosθ = FE/Fg
tanθ = qV/mgd
Projectile Motion in Uniform Electric Fields
The diagram below shows the plan view of an electron entering a uniform electric field along the centre line with initial velocity u.
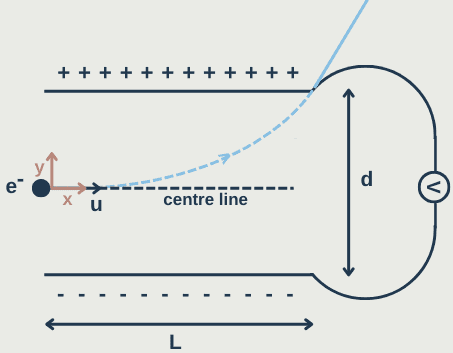
In the x-direction, the electron experiences no force so, Vₓ is constant = u. Using the suvat equation: s = ut+ 1/2 at², in the x-direction, x = ut.
In the y-direction, F = QV/d = eV/d (e is the charge on the electron).
As F = ma (Newton’s Second Law), a = eV/mₑd
(mₑ is the mass of the electron).
Since the force is constant and directed towards the positive plate, the electron will undergo uniform acceleration. Due to the constant acceleration in the vertical direction, and no forces acting in the horizontal direction, the electron will follow a parabolic path as it travels between the plates.
y-direction:
s = y
u = 0
v =
a = eV/mₑd
t = t
s = ut+ 1/2 at²
y = eVt²/2mₑd
Subbing in x = ut:
y = eVx²/2mₑdu²
Once the electron clears the plates and leaves the electric field, it no longer experiences any force due to the field. Since no forces are acting on the electron, it will continue moving in a straight line at a constant velocity (Newton’s First Law of Motion).
The velocity will have a horizontal and vertical component. The horizontal component will be the same as when it entered the field and the vertical component will have increased due to the acceleration in the field.
What is the minimum velocity e⁻ must enter with to clear the plates?
When the electron has travelled a length L in the x-direction, it has travelled d/2 up (in the y-direction).
We can substitute x = L and y = d/2 into our equation:
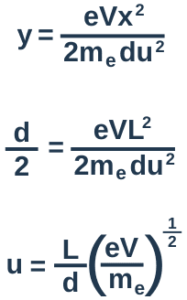
This is the minimum velocity with which the electron would need to enter the field to clear the plates.
Coulomb's Law
Coulomb’s Law is very similar to Newton’s Law of Gravitation which may make it easier to remember.
The force between 2 point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. It is a force of attraction between charges of opposite sign and a force of repulsion if the charges are of the same sign.
Air can be treated as a vacuum when calculating force between charges.
F ∝ Q₁Q₂
F ∝ 1/r²
ε₀ is the permittivity of free space (how well a medium can allow an electric field to develop) and has the value 8.85 x 10⁻¹² Fm⁻¹
1/4πε₀ is a constant (think of it is as the gravitational constant G)
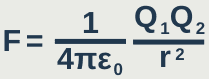
Coulomb's Law
The force between 2 point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.
Comparing the Magnitude of the Gravitational and Electromagnetic Force
To determine the ratio of the electromagnetic force to the gravitational force between two protons at any separation, we can divide one of the equations by the other (we want our answer to be in the form FE : Fg).

e is the charge on a proton = 1.60 x 10⁻¹⁹
mₚ is the mass of a proton = 1.67 x 10⁻²⁷
r² cancels out and we can start rearranging and substituting in:
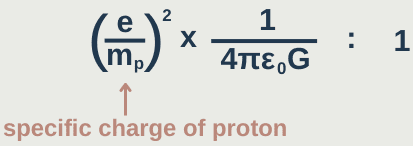
(9.58 x 10⁷)² x 1/(4π x 8.85 x 10⁻¹² x 6.67 x 10⁻¹¹) : 1
1.24 x 10³⁶ : 1
The electromagnetic force is roughly 10³⁶ times greater than the gravitational force. FE >> Fg
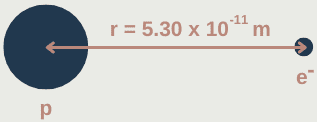
When a hydrogen atom is in its ground state, the radius of orbit of the electron is 5.30 x 10⁻¹¹ m. Calculate the linear speed of the electron and the number of orbits it completes in one second.
Centripetal force = Force between two charges
mₑv²/r = e²/4πε₀r²
So, v = √(e²/4πε₀rmₑ)
By square rooting e²/4, we can take them out of the square root sign (this may make calculations easier):
v = e/2 x √(1/πε₀rmₑ)
Substitute in the values:
v = (1.6 x 10⁻¹⁹)/2 x √(1/(π x 8.85 x 10⁻¹² x 5.30 x 10⁻¹¹ x 9.11 x 10⁻³¹))
v = 2.18 x 10⁶ ms⁻¹ = speed of inner orbital electron
The number of orbits it completes in one second = frequency
v = 2πrf
f = v/2πr
f = 2.18 x 10⁶/(2π x 5.30 x 10⁻¹¹)
f = 6.56 x 10¹⁵ Hz
What is the de Broglie wavelength?
λ = h/mv
λ = 6.63 x 10⁻³⁴ / (9.11 x 10⁻³¹ x 2.18 x 10⁶)
λ = 3.33 x 10⁻¹⁰ m
How does this compare with the circumference of orbit?
Circumference = 2πr = 2π x 5.30 x 10⁻¹¹
Circumference = 3.33 x 10⁻¹⁰ m
Electric Field Strength
The diagram below shows a square with sides of length a. There are four charged points on each corner of the square. You can imagine the point P is a particle with charge +q.
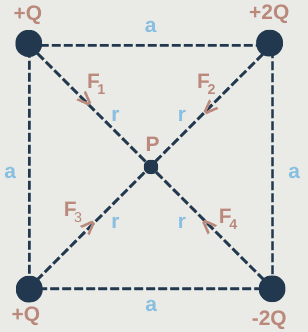
Find the magnitude and direction of the electric field at the centre of the square (P).
We can use Coulomb’s Law for each force (F₁, F₂, F₃, F₄) and then resolve to find the resultant force.
To find r (the distance between the centres of the points), we can use Pythagoras’s theorem:
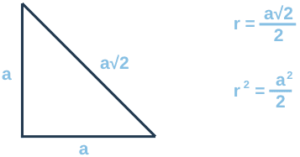
Now we have a value for r² which we can use in our equation.

F₁ = 2Qq/4πε₀a² = Qq/2πε₀a²
We are subbing in r² = a²/2, dividing by r² flips the fraction.
F₂ = Qq/πε₀a²
This is double F₁.
F₃ = Qq/2πε₀a²
F₄ = -Qq/πε₀a²
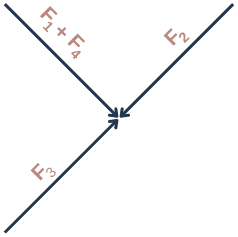
As F₄ is negative, resolving in one direction results in F₁ – (-F₄) = F₁ + F₄.
F₁+ F₄ = Qq/2πε₀a² + Qq/πε₀a² = 3Qq/2πε₀a²
Now we need to subtract F₃ from F₂.
F₂ – F₃ = Qq/πε₀a² – Qq/2πε₀a² = Qq/2πε₀a²
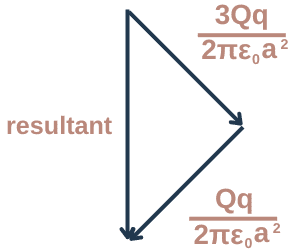
To find the resultant force we can use Pythagoras again, it will be easier to let Y = Qq/2πε₀a². Y is a random variable.
√((3Qq/2πε₀a²)² + (Qq/2πε₀a²)²)
This is the same as:
√((3Y)² + (Y)²) = √(9Y² + Y²) = √(10Y²)
We can sub Y = Qq/2πε₀a² back into the resultant force:
Qq/2πε₀a² x √(10)
Finally, to find the magnitude of the electric field strength we can use the equation: F = EQ
Eₙₑₜ = Fₙₑₜ / q
Eₙₑₜ = Q/2πε₀a² x √(10)
To find the direction we would use trig.
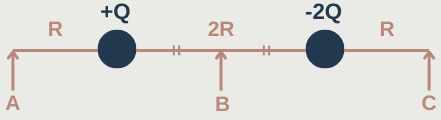
What is the electric field strength at each point? (A, B, C)
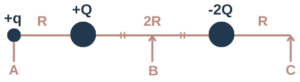
Point A:
Qq/4πε₀R² (to the left)
2Qq/4πε₀(3R)² = Qq/18πε₀R² (to the right)
FA = 1/4 – 1/18 = 7/36
FA = 7Qq/36πε₀R²
As F = EQ,
EA = FA/q
EA = 7Q/36πε₀R² (to the left)
Point B:
Now imagine there is a point charge (+q) at point B.
Qq/4πε₀R² (to the right)
2Qq/4πε₀R² = Qq/2πε₀R² (to the right)
FB = 1/4 + 1/2 = 3/4
FB = 3Qq/4πε₀R²
EB = 3Q/4πε₀R² (to the right)
Point C:
Now imagine there is a point charge (+q) at point C.
2Qq/4πε₀R² = Qq/2πε₀R² (to the left)
Qq/4πε₀(3R)² = Qq/36πε₀R² (to the right)
FC = 1/2 – 1/36 = 17/36
FC = 17Qq/36πε₀R²
EC = 17Q/36πε₀R² (to the left)
Electric Potential
In moving a charge q from an equipotential V to another at V + ΔV, the work done is qΔV and is independent of the path taken.
Absolute electric potential: the work done per unit positive charge in moving it to a point from infinity.
Graphical representations of Electric Potential
TO BE CONTINUED
